Fantasy Football Forecasting Pt. I

In search of a project for R, I’ve started fantasy football forecasting. I binge on FF already — spending hundreds of hours per season on leagues with payouts in the hundreds of dollars. I might as well learn something.

My goals are to 1) predict player’s fantasy points for the upcoming season and 2) create a draft ranking using the standard value-over-replacement.

Github repo: https://github.com/JJTimmons/ff

Scraping and cleaning

My repo is setup with just a few folders right now: data (immutable), analysis (scripts), and output (eg images for this post).

For input data in these early models, I’m using pro-football-reference. They have decades worth of fantasy football stats (last year’s: https://www.pro-football-reference.com/years/2017/fantasy.htm).

scrape_year <- function(year) {
  url <- paste0("https://www.pro-football-reference.com/years/", year, "/fantasy.htm")
  page <- read_html(url)

  player_table <- page %>%
    html_nodes("#fantasy") %>%
    html_table()
  player_table <- player_table[[1]] # only one per page

  headers <- player_table[1,] # first row is headers
  headers[2] <- "Name" # blank by default
  colnames(player_table) <- headers # set headers
  player_table <- player_table[nchar(player_table$Name) > 1, ] # remove title rows
  player_table <- data.frame(player_table)

  player_table$Year <- rep(year, nrow(player_table)) # set year in the Year column
  player_table
}

FIRST_YEAR <- 1997
LAST_YEAR <- 2017
player.data <- lapply(seq(from=FIRST_YEAR, to=LAST_YEAR), scrape_year)
player.data <- do.call(rbind, player.data) # https://www.r-bloggers.com/concatenating-a-list-of-data-frames/
save(player.data, file = paste0("player_data.raw.Rda"))

After some cleaning and type setting (not shown), the data was ready for basic modeling.

Panel data and plm

I spent a couple days unsure about how to go about forecasting. At first I created a basic for loop that simply lagged the each player’s fantasy points, but I was unclear on how to create regressions.

It would have been trivial had every player played the same seasons (ie if the data-set had been “balanced,” a new word for me). But the players, of course, didn’t play for the same season. I scraped 20 years of fantasy data, and the average running back’s career is just 2.5 years. An aside: the longest NFL career in history was 26 seasons — it was George Blanda’s. He was also the oldest person to have played in the NFL (he retired at 48!).

What I needed was a way to regress fantasy points scored on lagged covariates in an apples vs apples way across time. Some course notes had the name for this type of data-set:

Panel data (also known as longitudinal or cross-sectional time-series data) is a dataset in which the behavior of entities are observed across time.

This data type fits fantasy football stats perfectly and, because of that, I settled on R’s plm package. After converting the data to a pseries object I was ready to create regressions by position. An example for quarterbacks:

setwd("~/Documents/GitHub/ff/analysis")
load("~/Documents/GitHub/ff/data/player_data.Rda")

# only a decade's worth of data
player.data <- player.data[player.data$year >= 2007,]
player.data <- pdata.frame(player.data, index=c("name","year"), drop.index=FALSE, row.names=TRUE)
player.data <- split(player.data, player.data$fantpos)

qb.data <- player.data[["QB"]]
qb.formula <- formula(fantpt ~ lag(fantpt) + age)
qb.model <- plm(qb.formula, data = qb.data, index = c("name","year"), model="pooling")
summary(qb.model)

# for each player in the data set
qb.coors <- data.frame(x=numeric(0), y=numeric(0))
med.pts <- median(qb.data$fantpt, na.rm = TRUE)
for (name in unique(qb.data$name)[1:30]) {
  player <- qb.data[qb.data$name == name, ]

  for (i in 1:nrow(player)) {
    # if there's no data on player last year, skip
    if (i-1 < 1) next

    player.now <- player[i,]
    lag1 <- player[i-1, "fantpt"]

    qb.coors <- rbind(
       qb.coors,
       list(
          x = sum(c(1, lag1, player.now$age) * qb.model$coefficients, na.rm = TRUE),
          y = player[i+1,"fantpt"]
       )
    )
  }
}

# only keep the cases where we know next season's score
qb.coors <- qb.coors[complete.cases(qb.coors),]

# calculate R-squared
total <- with(qb.coors, sum((y - mean(y))^2))
var <- with(qb.coors, sum((y - x)^2))
qb.rsqrd <- round(1 - (var / total), digits = 3)
qb.rsqrd <- paste0("R^2 = ", qb.rsqrd)
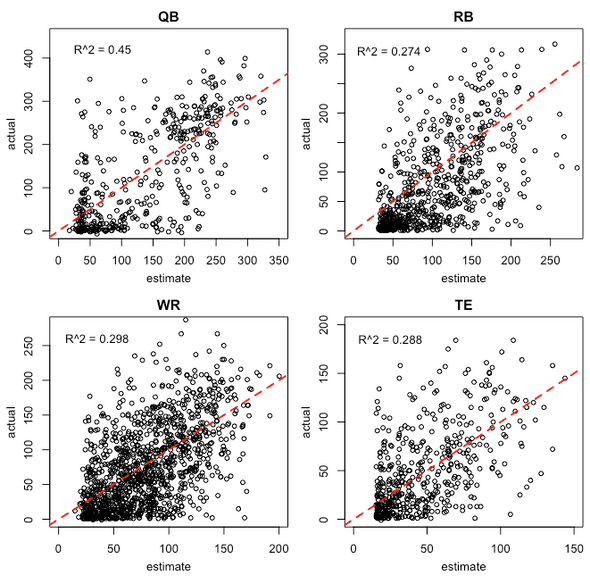
qb.rsqrd

Unfortunately, given the weekend, I wasn’t able to find any model (for QBs, RBs, WRs, and TEs) that did better than a simple regression on lagged fantasy points and age — and age had a very small effect. In other words, by far the best predictor for next year’s points was last year’s points.

Coefficients for QB model:
             Estimate Std. Error t-value  Pr(>|t|)
(Intercept) 73.238273  24.619189  2.9748  0.003073 **
lag(fantpt)  0.744202   0.031641 23.5200 < 2.2e-16 ***
age         -1.419620   0.847950 -1.6742  0.094722 .
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

An obvious negative to this kind of prediction is that it narrows the model’s applicability to players with a previous year’s data to reference. So newly drafted players won’t show up at all. I tried a step-wise function, where I imputed the median for a rookie player into the previous years results, but it negatively affected the R-squared of every position.

The model is also biased in that we’re only regressing data from players that played in the “next” season. For example, players that had bad seasons — perhaps those ended by season-ending injuries — are underrepresented in the model, which I think is part of the reason the expected pts coefficient is so high for all of the models.

Future

The models are uber-simplistic. Given that their predictive power comes duplicating what the player got the year before, they are hardely useful. But it’s also just a first draft approach. In the future, I’ll try to incorporate additional information.

The easiest approach would be to incorporate “expert opinions” — adding in draft predictions from ESPN, NFL, CBS, etc. This is the most conventional approach (see: fantasyfootballnerd.com, fantasyfootballanalytics.net, fantasypros.com) and is also the most robust, according to Fantasy Football Analytics. This makes sense, since the results of accumulating everyone’s predictions is something like that of a meta-analysis.

Another approach, that I haven’t seen anyone do, would be to add in meta from Madden to see if their player stats (like skill primitives) are enough to help predict outcome. Or maybe Madden stats plus expert ratings… To be continued.